Walk the Walk

Basically what lately did put pathtraced SSS into production is the understanding that we're more interested in calculating the solution to our random walks at the surface boundaries instead of wasting time and efforts with paths that ain't making relevant contributions to the image. We always did know that but before some late research we were not aware on how to do it.. the problem was that we needed an improved importance sampling which we call here without further digging.. zero variance-based sampling scheme (aka Dwivedi sampling).

The only problem with this is that the scheme makes some assumptions like considering all geometry a flat, semi-infinite medium.. called half-space (what you just see below).

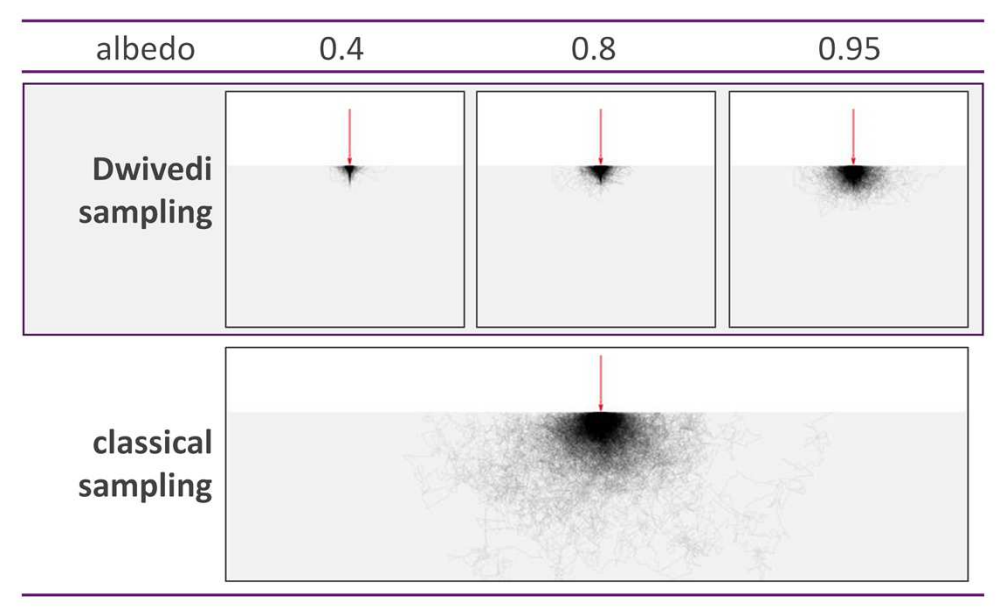
Of course our geometry is not always an half-space. We have curvature and geometry slabs where paths are supposed to be able to exit from the bottom boundary (ie. for thin ear geometry). Because of this, Dwivedi sampling is never fully employed but left at around 75% of utilization where the other 25% is the classic unbiased sampling that will better cover those corner cases.. as both schemes are chosen stochastically (ie. randomly) we have good chances to always converge to an optimal SSS solution. However there're also cases where we can go full 100% Dwivedi because of how the geometry is.

This is why we left up to you to fully control the mechanism. With the Guided Walk parameter we can go full classic with a value of 0 or fully Dwivedi with a value of 1. Sometime we can get incredibly better SSS quality just matching the best value for the geometry we have. A value of 0.75 is the default value used in the original papers so if you ain't grasping what it is used for you can simply ignore it completely. But if you do, take care that it is fully texturable.. so we can even dinamically control, based on the underlying geometry (with for example curvature or occlusion shaders), what to do pixel by pixel.

Another parameter that make a difference when we don't have thin slabs and such is 'Check Opposite Side'. When this param is not enabled we have way better convergence because Dwivedi sampling won't be required to be put into a multiple importance sampling mechanism deteriorating its influence because of the added probability choice on what side we should direct our random walks. 

Eventually our own contributions to the state-of-the-art of subsurface scattering are regarding the boundary selection and the utilization of a more tailored light vector that will act as a surface boundary normal for difficult to sample cases.

The former is based on what we called the 'd'Eon's probability' + the 'Meng's Closest Point'. Because in thin-slabs like ear geometry we have two boundaries where our paths can find an escape.. Meng(et al. 2016) suggested to use a kind of heuristic where we use the closest point normal as boundary normal. Eugene d'Eon instead lately used a more theoretical approach suggesting a probability scheme to employ for better importance sampling. Turns out that a nice improvement to sample SSS with guided (zero-variance) walks is to use Meng's closest point and normal heuristics and then the d'Eon's forward/backward probability to stochastically account for the boundary choice. Our contribution is to use both strategies for improved quality.

Then there's the intuition to use Meng's closest point + d'Eon's probability + an incident illumination vector modeled similar to Walter's (et al. 2009) half-vector formulation.. this gives better sampling for thin-slabbed geometry.. like those presumably delicious chocolate rolls on top of the cake.. there, an entering path should have more chances to exit from the backward boundary and then to use an incident illumination vector instead of the geometry normal. You can tell the shader to use this strategy by using Incident Light Vector parameter. Being a 0-1 floating slider it is super easy to use a texture (which generally is the SSS map we may already use) to map thin parts like ears nostrils eyelids for improved SSS sampling quality.

Take care that while it may look we aren't getting so much of a better SSS solution.. at these levels of convergence just a marginal gain in quality like this one is a big achivement as it will drastically cut render times in those areas because effectively all the other parts are already almost fully converged.

Now beside Color Radius and Anisotropy which remain the same as the Standard Material SSS we have the Radius parameter that is exactly 10x bigger when compared with Standard SSS. Which also means we can have a 10x more little radius to catch more details. Practically if we have a previously setup SSS with the Standard Material we can simply do a x10 to get almost the same overall appearance.. ie. a 0.1 radius with Standard Material is a 1.0 radius with SSSRandomWalk. 

We're left with the Translucency parameter. This will completely change the underlying exponential behaviour of our random walks turning them into non-exponential walks. Non-exponential random walks are great to simulate plastics and other polymers, the discoloration and drying of certain natural materials or because of their long-range correlations they are able to model thin-walled materials like those used below. 

For skin, they are particulary good to model dryed up skin like that around nostrils and also up to some percentage to model the overall behaviour of general skin that being made of multiple layers is hardly just exponential in nature.. we used a general 25% (0.25) for the skin below and mapped a 0.50 to nostrils and skin around the mouth. Take care that non-exponential random walks are a bit slower to converge than default exponential walks so if your main focus is on pure speed, leave this param at 0.

Eventually take a look at Improved SSS page to see additional parameters that have been added more recently... like Mie/Rayleigh scattering together with a full set of parameters to better control SSS in GI indirect lighting and the availability to select different Albedo remapping strategies to better match some kind of renditions.